[Dynamic Programming] They are Tabonacci numbers, not Fibonacci numbers

Problem: 1137. Nth Tabonacci number

Article directory

• Question interpretation
• Problem solving method
• • dp dynamic programming
  • Iterative optimization?
• the complexity
• Code

Explanation of the question

First, let’s explain the meaning of this question

• I believe that when readers see [Tepbonacci Numbers], they can’t help but think of [Fibonacci Numbers]. They are twin brothers. This Tepbonacci Number is equivalent to >An enhanced version of Fibonacci Numbers
• We can first see this recursive formula Tn + 3 = Tn + Tn + 1 + Tn + 2. Readers may not understand it well, so we will convert it into Tn = Tn-1 + Tn-2 + Tn-3, that is, all n are unified -3. Then the Nth Tabonacci number is equal to the sum of the previous three Tabonacci numbers

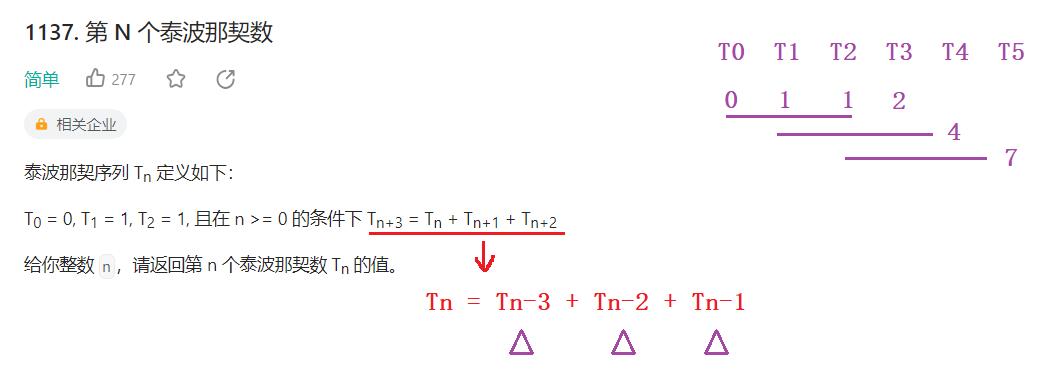
• Seeing T3 above, the sum of the first three numbers is equal to 2. By analogy, T4 is T1 + T2 + T3 = 4

Problem-solving methods

After reading the above analysis of the problem, I will introduce two solutions below

dp dynamic programming

First of all, the key point that needs to be mastered in this problem is the solution of [Dynamic Programming]. We have to divide it into five steps to solve it.

1. Status representation

• First of all, readers should be clear that when solving dynamic programming problems, a dp array is needed, so the meaning of [state representation] is the meaning of the value in the dp table.

So where does this status representation come from?

① The first one is to follow the question requirements, that is, dp[i] represents the value of the i-th Tabonacci sequence

② The second one requires readers to have rich experience in answering questions, so that they can get the corresponding results after reading the questions.

③ The third one is that in the process of analyzing the problem, repeated sub-problems are found

If readers have been exposed to similar dynamic programming problems before, they will see some problem explanations explaining: What is the state representation of this problem, and then we will directly talk about the state representation of this problem. EquationIt doesn’t say at all how the state representation of this question comes from. I will explain this process in other dynamic programming topics.

Therefore, when solving similar problems, readers must know how the following [state representation equation] comes from, and “know what it is, know why it is so”

2. state expression equation

• Then the state expression equation of this question is dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

3. initialization

• After knowing how to write the [state representation equation], what we have to do is to initialize the dp array. Seeing the dp array below, if our subscript value reaches 0 at the beginning, then i - 1, i - 2, i - 3, these will cause cross-border

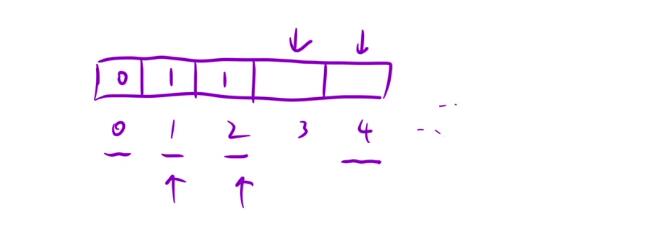
• Therefore, we need to initialize this dp array. Specifically, we need to initialize the first three data, namely dp[0], dp[1], and dp[ 2] are initialized to [0][1][1] respectively, then when we traverse and calculate later, we only need to start from the position with subscript 3.

 dp[0] = 0, dp[1] = dp[2] = 1;

4. Order of filling in the form

• The next step is to fill the dp array according to the state representation equation

for(int i = 3; i <= n; + + i)
{<!-- -->
    //State transition equation
    dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
}

5. return value

• In the last part, we deal with the return value. According to the question requirements, we want to return [the value of the nth Tabonacci number Tn], so just return dp[n]

However, if you only consider the above, there will be an out-of-bounds situation when submitting, because the range of n given in the question is [0, 37], so for dp[0]It’s easy to say, but the subsequent data will be out of bounds.

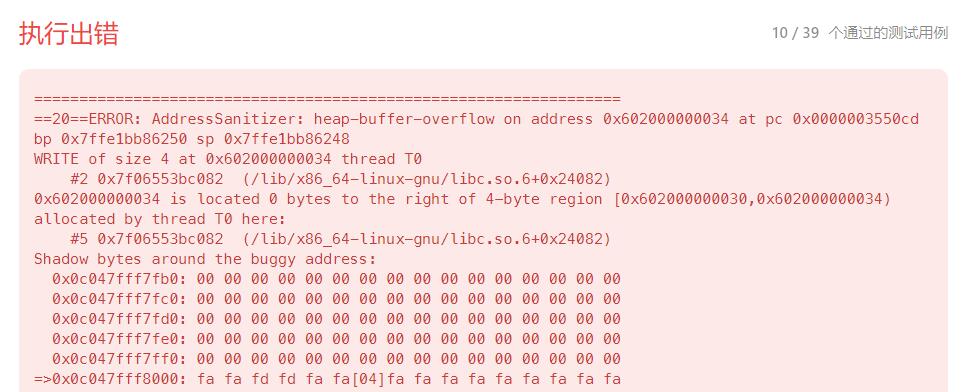
Therefore, we also need to consider some boundary issues

//Boundary issue processing
if(n == 0) return 0;
if(n == 1 || n == 2) return 1;

The overall code will be given at the end

Iterative optimization?

After reading the above one, let’s see if it can be optimized

• If the reader has been exposed to iterative algorithms, he should be able to quickly think of the idea of this question. Because it is an accumulation of three by three, we can define three variables here: a, b, c, their accumulated values can be placed in the variable d

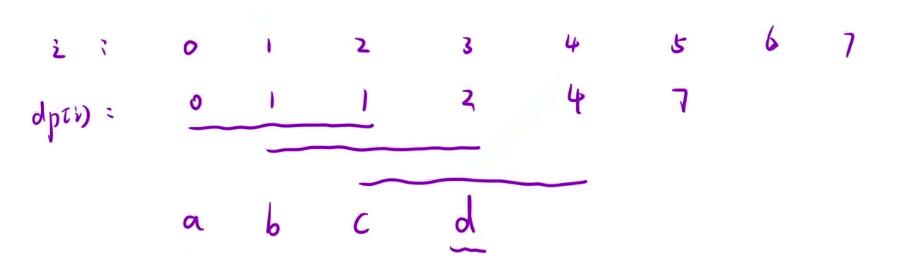
• Therefore, after one round of accumulation, we need to perform an iterative operation

a = b; b = c; c = d;

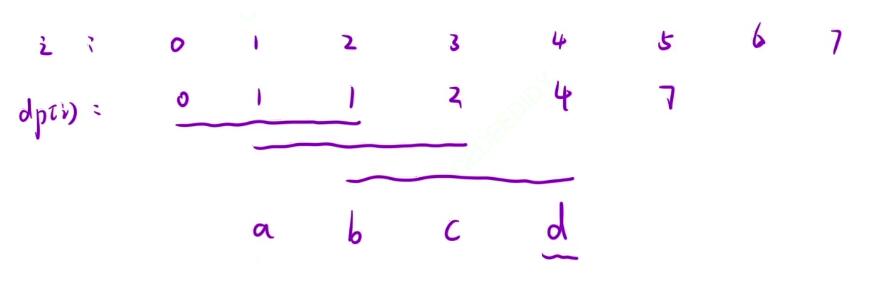
• Then the value we need to return in the end is this d

return d;

Complexity

• time complexity:

For the first solution to dp, its time complexity is

O

(

n

)

O(n)

O(n), and the time complexity of the second iteration solution is

O

(

1

)

O(1)

O(1)

• Space complexity:

For the first solution to dp, its space complexity is

O

(

n

)

O(n)

O(n), and the time complexity of the second iteration solution is

O

(

1

)

O(1)

O(1)

So based on this comparison, the method of iterative optimization is still worth mastering.

Code

The first is the solution to the first dp dynamic programming

class Solution {<!-- -->
public:
    int tribonacci(int n) {<!-- -->
        // Handling boundary issues
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;
        // 1. Create dp table
        vector<int> dp(n + 1);

        // 2.Initialization
        dp[0] = 0, dp[1] = 1, dp[2] = 1;

        // 3. Fill in the form
        for(int i = 3; i <= n; + + i)
        {<!-- -->
            //State transition equation
            dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
        }

        // 4.Return value
        return dp[n];
    }
};

Then there is the second method of using iterative optimization

class Solution {<!-- -->
public:
    // space optimization
    int tribonacci(int n) {<!-- -->
        //Special case handling
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;
        int a = 0, b = 1, c = 1, d = 0;
        for(int i = 3; i <= n; + + i)
        {<!-- -->
            d = a + b + c;
            // iterate
            a = b; b = c; c = d;
        }
        return d;
    }
};