Table of Contents
Preface: Summary of issues related to the Fibonacci sequence
1. Find the nth term of the Fibonacci sequence (iterative + recursive double solution)
1.What is Fibonacci Sequence
1.1. Introduction
1.1.1.Definition
1.1.2 Form
widely used:
2. Iterative method:
2.1 Ideas
2.2 Code implementation
3. Recursive method:
3.1 Ideas
3.2 Code implementation
2. The problem of frog jumping up steps
1.Title description;
2. Idea analysis
We can use recursive or dynamic programming to solve this problem.
3. Method 1: Recursive method
3.1 What is recursion
3.2 Recursive problem-solving ideas
3.3 Code implementation
4. Method 2: Use dynamic programming
4.1 What is dynamic programming
4.2 Dynamic programming problem-solving ideas
4.3 Code implementation
5. The difference between dynamic programming and recursion
5.1 Recursion:
5.2 Dynamic programming
postscript
Foreword: Summarizing the related issues of the Fibonacci Sequence
Summary of learning, I hope it can also help you. Welcome to follow my blog! Wonderful content will be continuously updated!
HI~ This is my blog link! Please pay attention to Sanlian so you don’t get lost in the future~
Your likes/collections/comments are the motivation for my progress!!!
1. Find the nth term of the Fibonacci sequence (iterative + recursive double solution)
1. What is the Fibonacci sequence
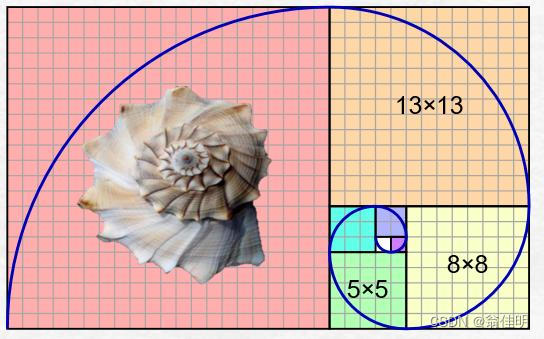
1.1. Introduction
The Fibonacci sequence, also known as the golden section sequence, was introduced by the mathematician Leonardo Fibonacci using rabbit reproduction as an example, so it is also called the “rabbit sequence”. It is: 1, 1, 2, 3, 5, 8, 13, 21, 34… Mathematically, this sequence is defined by the following recursive method: F(0)=1, F(1)=1, F(n)=F(n – 1) + F(n – 2) (n ≥ 2, n ∈ N*).
Starting from the third term, each term is equal to the sum of the previous two terms, in which the initial two numbers are 0 and 1 respectively.
1.1.1.Definition
Fibonacci Sequence refers to a sequence of numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
Fibonacci numbers in nature
This sequence starts with item 3, and each item is equal to the sum of the previous two items.
- When n=0, the 0th term of the Fibonacci sequence is 0;
- When n=1, the first term of the Fibonacci sequence is 1;
- When n>1, the nth term of the Fibonacci sequence is the sum of the (n-1)th term and the (n-2)th term.
1.1.2Form
The first few numbers in the Fibonacci sequence are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
Widely used:
The Fibonacci sequence is widely used in mathematics and computer science. For example, it can be seen in algorithm design, cryptography, stock analysis, music rhythm and other fields.
2. Iteration method:
2.1 Idea
First determine the preconditions, and then iterate the subsequent values in sequence
2.2 Code Implementation
public static int fibonacciNumbers(int n) {
int first = 0; //Determine the 0th and 1st items
int second = 1;
int result = 0;
if (n == 0) {
result = first; //When the number of items is 0, return the number on item 0
} else if (n == 1) { //When the number of items is 1, return the number on item 1
result = second;
} else {
for (int i = 2; i <= n; i + + ) { //Starting from the second item, the result of the number of items is equal to the sum of the first two items
result = first + second; //iterate the values of the first two items respectively
first = second;
second = result;
}
}
return result;
}
3. Recursive method:
3.1 Idea
Use recursion to continuously decompose the problem, violently and directly, reduce the complex into simplicity, and reduce the whole into parts.
3.2 Code Implementation
public static int fibonacciNumbers(int n) {
if(n==0){
return 0;
} else if (n==1) {
return 1;
}else{
return fibonacciNumbers(n-1) + fibonacciNumbers(n-2); //Through recursion, continue to decompose the nth item and weaken it into the conditions of the first two items
}
}
2. Frog jumping up steps problem
1.Title description;
The frog jumping problem is a classic recursive problem that can be solved using recursion or dynamic programming. The frog can jump up to 1 or 2 steps at a time. How many different ways can the frog jump up to n steps?
2. Idea analysis
Assume that the number of ways a frog can jump up n steps is F(n), then there are two situations:
1. If the frog jumps 1 step for the first time, then there are n-1 more steps to jump, and the number of jumps is F(n-1).
2. If the frog jumps 2 steps for the first time, then there are n-2 steps to jump, and the number of jumps is F(n-2).
Therefore, the total number of jumps F(n) for the frog to jump up n steps is equal to the sum of the number of jumps in the first two situations, that is, F(n) = F(n-1) + F(n-2). This is the definition of the Fibonacci sequence.
We can use recursion or dynamic programming to solve this problem.
3. Method 1: Recursive method
3.1 What is recursion
Recursion can divide complex problems into simpler sub-problems, making the solution of the problem simpler.
During recursion, the function calls itself multiple times, each solving a smaller subproblem, until the base case (termination condition) is reached. Then, based on the solutions to the sub-problems, the original problem is gradually solved, and finally the solution to the entire problem is obtained.
3.2 Recursive problem-solving ideas
In this recursive method, we first determine if n is less than or equal to 2, and return n directly. Otherwise, according to the recursive formula F(n) = F(n-1) + F(n-2), recursively call the jumpFloor function to solve the results of F(n – 1) and F(n – 2), and return their and.
3.3 code implementation
public static int jumpFloor(int n) {
if (n <= 2) {
return n;
}
return jumpFloor(n - 1) + jumpFloor(n - 2);
}
4. Method 2: Use dynamic programming
4.1 What is dynamic programming
Dynamic Programming is a commonly used optimization method to solve multi-stage decision-making problems. It reduces time complexity by dividing the original problem into several sub-problems and saving the solutions to the sub-problems to avoid repeated calculations.
4.2 Dynamic programming problem-solving ideas
In the dynamic programming method, an array arr with a length of n + 1 is created to save the number of jumps corresponding to each step. Initialize arr[1] to 1 and arr[2] to 2, and then starting from the third step, calculate the value of each step according to the recursive formula F(n) = F(n-1) + F(n-2) Jump method number and store it in the arr array, and finally return arr[n].
4.3 Code Implementation
public static int jumpFloor(int n) {
if (n <= 2) {
return n;
}
int[] arr = new int[n + 1];
arr[1] = 1;
arr[2] = 2;
for (int i = 3; i <= n; i + + ) {
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[n];
}
5. The difference between dynamic programming and recursion
5.1 Recursion:
The way recursion is implemented is to solve the problem by continuously calling itself through the function, dividing the complex problem into smaller sub-problems, each recursive call solves one sub-problem, and finally obtains the solution to the entire problem. Recursion usually takes up more space and time, because each recursive call creates new stack frames, which require additional memory space, and the efficiency of recursion is also limited by the call stack.
5.2 Dynamic Planning
Dynamic programming is implemented by splitting the original problem into multiple overlapping sub-problems and saving the solution of each sub-problem to avoid repeated calculations and reduce time complexity. Dynamic programming is generally suitable for problems with overlapping subproblems and optimal substructure properties. Overlapping subproblems refer to the fact that the same subproblem is calculated multiple times when solving the problem, while optimal substructure refers to the fact that the optimal solution to the problem can be constructed from the optimal solutions to the subproblems. Dynamic programming is highly efficient because it only needs to calculate each subproblem once, avoiding the cost of repeated calculations.
Postscript
Learning means constantly summarizing, and I hope it can help others.
If you see this, please support me, thank you~
